Usage¶
Listing synthesis runs¶
This section only applies to HDF5 datasets. If you are using the FITS format, you have one FITS file per galaxy per run.
Start a python shell. To list the synthesis runs present in the database qalifa-synthesis.h5, use the function listRuns():
>>> from pycasso.h5datacube import
>>> listRuns('qalifa-synthesis.h5')
eBR_v20_q027.d13c512.ps3b.k1.mC.CCM.Bgsd01.v01
eBR_v20_q036.d13c512.ps03.k2.mC.CCM.Bgsd61
In this case, we have two runs, 'eBR_v20_q027.d13c512.ps3b.k1.mC.CCM.Bgsd01.v01' and 'eBR_v20_q036.d13c512.ps03.k2.mC.CCM.Bgsd61'. The other tools for listing the contents of a database are listBases() and listQbickRuns().
>>> listBases('qalifa-synthesis.h5')
Bgsd01 Bgsd61
>>> listQbickRuns('qalifa-synthesis.h5')
q027 q036
Now, we can search the runs that have specific bases or qbick runs using the keyword arguments baseId and qbickRunId. One can specify any one or both of these filter arguments.
>>> listRuns('qalifa-synthesis.h5', baseId='q036', qbickRunId='Bgsd61')
eBR_v20_q036.d13c512.ps03.k2.mC.CCM.Bgsd61
Loading galaxy data¶
To load the galaxy 'K0001' (IC5376), in the run 'eBR_v20_q036.d13c512.ps03.k2.mC.CCM.Bgsd61' from the database, do
>>> from pycasso.h5datacube import
>>> K = h5Q3DataCube('qalifa-synthesis.h5', \
'eBR_v20_q036.d13c512.ps03.k2.mC.CCM.Bgsd61', 'K0001')
The object K is a h5Q3DataCube. which implements IQ3DataCube. The latter defines high level algorithms like zone to spatial conversions and radial profiles, while the former contains the I/O related stuff. If you are using ipython, entering K followed by two tab keystrokes, you should see all the properties of the galaxy and all methods available to operate on those.
If you have FITS files with your data, please refer to Loading from FITS files.
Zone smoothing¶
The data from the galaxies are are binned in spatial regions called voronoi bins. There is a procedure called “dezonification” which converts the data from voronoi bins back to spatial coordinates. When doing so, one can use the surface brightness of the image of the galaxy as a hint to smooth some of the properties.
This is enabled by default. To disable it, set the keyword argument smooth to False when loading the galaxy.
>>> K = h5Q3DataCube('qalifa-synthesis.h5', \
'eBR_v20_q036.d13c512.ps03.k2.mC.CCM.Bgsd61', 'K0001', smooth=False)
For more information, see getDezonificationWeight().
Displaying property images¶
In this section we explain how to obtain images of properties of the galaxy. Most of of the properties of interest are already calculated, see the section Galaxy property list.
Here we assume the galaxy is loaded as K. Now, all the data is stored as voronoi zones, but we really want to see the spatial distribution of the galaxy properties. K has a method for converting data from voronoi zones to images, the method zoneToYX().
Let’s see the property popx. It is a 3-dimensional array, containing the light fraction for every triplet (age, metallicity, zone).
>>> K.popx.shape (39, 4, 649) >>> K.N_age, K.N_met, K.N_zone (39, 4, 649)
Now, we want to see how this is distributed in the galaxy. The fraction of light in each population is the same in every pixel of a zone. So, we call popx an intensive property. To inform zoneToYX() that the property is intensive, we set extensive=False.
>>> popx = K.zoneToYX(K.popx, extensive=False) >>> popx.shape (39, 4, 72, 77)
In this case, the resulting popx is 4-dimensional, where the zone dimension has been replaced by the (x,y) plane. Let’s plot the young population (summing only the fractions for ages smaller than 1Gyr) as a function of the position in the galaxy plane.
>>> import matplotlib.pyplot as plt
>>> popY = popx[K.ageBase < 1e9].sum(axis=1).sum(axis=0)
>>> plt.imshow(popY, origin='lower', interpolation='nearest')
>>> cb = plt.colorbar()
>>> cb.set_label('[%]')
>>> plt.title('light fraction < 1 Gyr')
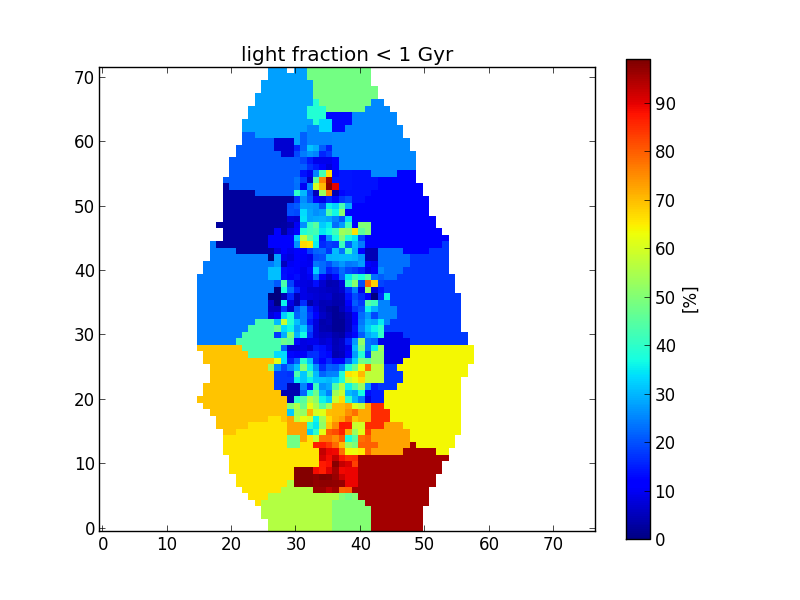
Masked pixels¶
The white pixels do not belong to any zone (masked pixels), and by default are set to numpy.nan. One might change the fill value for the masked pixels using the keyword fill_value. For example, to fill with zeros,
>>> popx_fill_zeros = K.zoneToYX(K.popx, extensive=False, fill_value=0.0)
It is recommended to use the fill values as nan, this way you know when you make a mistake and use values from regions where there’s no data (nan is contagious, any operation containing a nan will yield nan).
Surface densities¶
When the property is extensive, such as mass or flux, it is more proper to work with surface densities of these properties, when working with images. The most easily acknowledged extensive properties are light and mass. The properties Lobn__z, Mini__z and Mcor__z are the total light and mass for the voronoi zones. When we convert these to images, setting extensive=True, the resulting image contains the surface density of these properties (for example, in units of \(M_\odot / pc^2\)).
>>> McorSD = K.zoneToYX(K.Mcor__z, extensive=True)
>>> plt.imshow(McorSD, origin='lower', interpolation='nearest')
>>> cb = plt.colorbar()
>>> cb.set_label('$[M_\odot / pc^2]$')
>>> plt.title('McorSD')
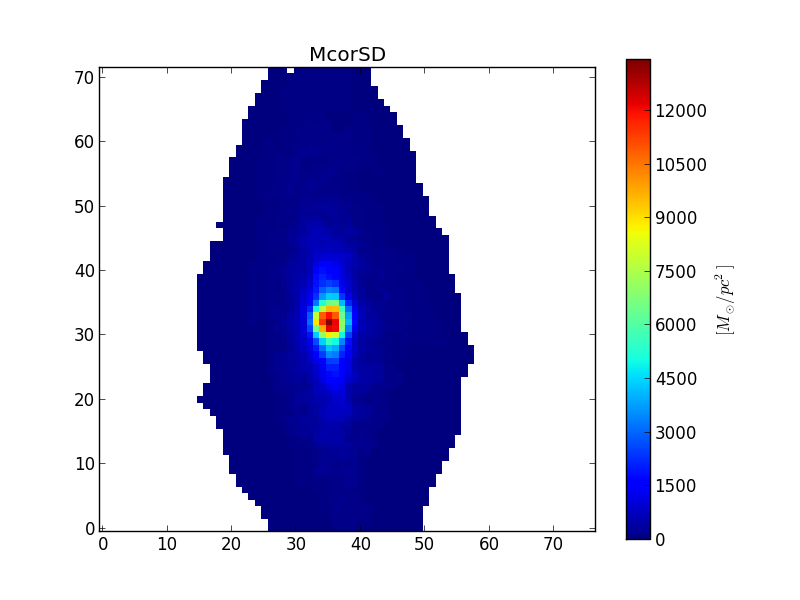
This is the same property as McorSD__yx, see the section below.
Predefined properties¶
The conversion from zones to images is perhaps the most common thing you wil ever use from PyCASSO. To make things easier (and less verbose), most of the properties already have been converted to images. These predefined properties take care of the extensiveness or intensiveness nature of the physical property, and return a surface density when suitable. The full list of propeties can be seen in the section Galaxy property list.
Radial and azimuthal profiles¶
Galaxy images are nice and all, but in the end you want to compare spatial information between galaxies, and it can not be done in a per pixel basis. One can think in polar coordinates and analyze only the radial variations of the properties. For this we have to think about what galaxy distances in these images really mean.
Image geometry¶
One fair approximation is to assume the galaxy has an axis-symmetric geometry. Therefore, if we see the galaxy as an elliptic shape, that is because of its inclination with respect to the line of sight. If we get all the points at a given distance a from the center of the galaxy, this will appear as an ellipse of semimajor axis equal to a.
To know the distace of each pixel to the center of the galaxy, we need to know the ellipticity (ba) of the galaxy, defined as \(\frac{b}{a}\) (ratio between semiminor and semimajor axes), and the position angle (pa, in radians, counter-clockwise from the X-axis) of the ellipse. These can be set using the method setGeometry(). The distance of each pixel is obtained using the property pixelDistance__yx.
>>> K.setGeometry(pa=45*np.pi/180.0, ba=0.75)
>>> dist = K.pixelDistance__yx
>>> plt.imshow(dist, origin='lower', interpolation='nearest')
>>> cb = plt.colorbar()
>>> cb.set_label('pixels')
>>> plt.title('Pixel distance')
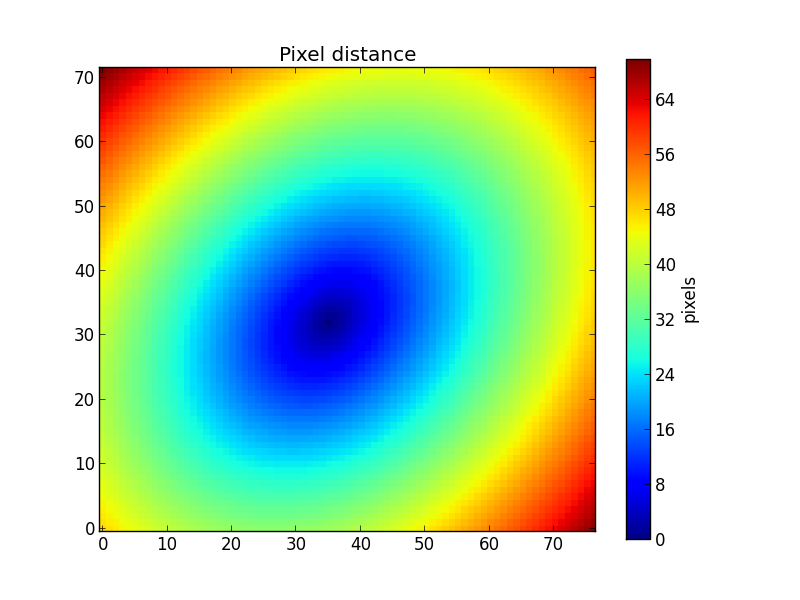
This example geometry clearly does not correspond to geometry of the galaxy, as seen in the previous figures. If we lack the values of ba and pa from other sources, we can use the method getEllipseParams() to estimate these ellipse parameters using “Stokes’ moments” of the flux (actually, we use qSignal) as explained in the paper Sloan Digital Sky Survey: Early Data Release.
>>> pa, ba = K.getEllipseParams()
>>> K.setGeometry(pa, ba)
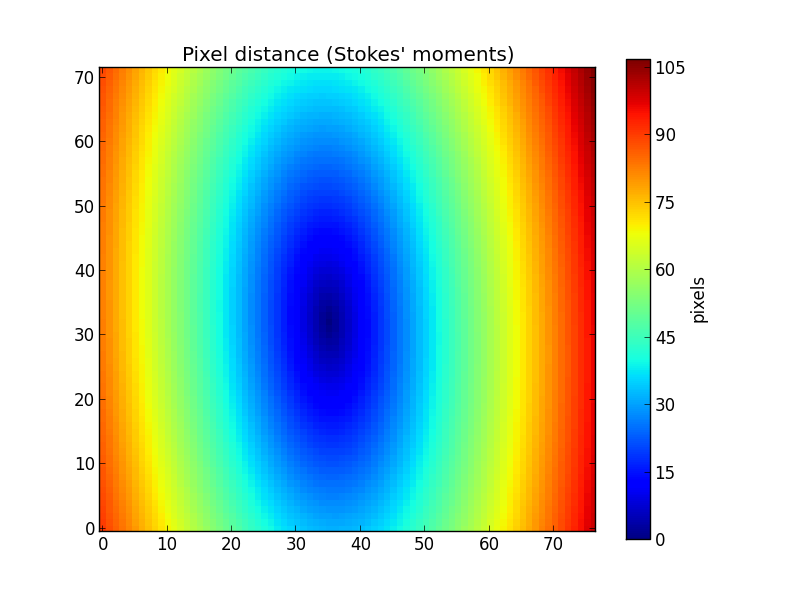
Now the distances match the geometry of the galaxy assuming it has an elliptical desitribution. Other parameters thar may be set by setGeometry() are the Half Light Radius (see below) and the center of the galaxy, by using respectively the keyword parameters HLR_pix and center (a tuple containing x and y).
Galaxy scales¶
We also need to take into account that galaxies exist in all sizes and distances. This means that using pixels as a distance scale is not satisfactory. Thus we have to convert distances to a “natural scale” to compare the radial profiles of distinct galaxies.
We define the Half Light Radius (HLR_pix) as the semimajor axis of the ellipse centered at the galaxy center containing half of the flux in a certain band. In PyCASSO, we use qSignal, which is the flux in the normalization window (\(5635\ \AA\)).
The HLR is updated whenever setGeometry() is called. One can explicitly set the HLR using the HLR_pix parameter, or let it be determined automatically. Note that the HLR depends heavily on the ellipse parameters.
- Circular
>>> K.setGeometry(pa=0.0, ba=1.0)
>>> K.HLR_pix
9.334798311419563
- Ellipse
>>> pa, ba = K.getEllipseParams()
>>> K.setGeometry(pa, ba)
>>> K.HLR_pix
12.878480006876336
>>> K.HLR_pc
2545.9657503507078
In the last line we show the HLR in parsecs (HLR_pc), which may be handy sometimes. It is based on HLR_pix and parsecPerPixel.
Alternatively, one can think in terms of other property as a half-scale. This is achieved using the method getHalfRadius(). One alternate scale commonly used is the mass. To calculate the Half Mass Radius (HMR) use the following:
>>> K.getHalfRadius(K.McorSD__yx)
7.612629351561292
The input for this method must be a 2-D image.
Note: This uses the same computation as the HLR.
Calculating the radial profile of a 2-D image¶
Now that we have a scale to measure things in radial distance, it is useful to have a radial profile of things. First, let’s assume we have a 2-D image we want to get the radial profile, for instance, at_flux__yx. The method radialProfile() receives a 2-D image of a given property, a set of radial bins, an optional radial scale (it uses HLR by default) and returns the average values of the pixels inside each bin. Think of it as a fancy histogram.
>>> HMR = K.getHalfRadius(K.McorSD__yx)
>>> bin_r = np.arange(0, 3+0.1, 0.1)
>>> bin_center = (bin_r[1:] + bin_r[:-1]) / 2.0
>>> at_flux__HLR = K.radialProfile(K.at_flux__yx, bin_r)
>>> at_flux__HMR = K.radialProfile(K.at_flux__yx, bin_r, rad_scale=HMR)
>>> plt.plot(bin_center, at_flux__HLR, '-k', label='HLR')
>>> plt.plot(bin_center, at_flux__HMR, '--k', label='HMR')
>>> plt.ylabel(r'$\langle \log t\rangle$')
>>> plt.xlabel(r'$R_{50}$')
>>> plt.title('Radial profile of the mean stellar age')
>>> plt.legend()
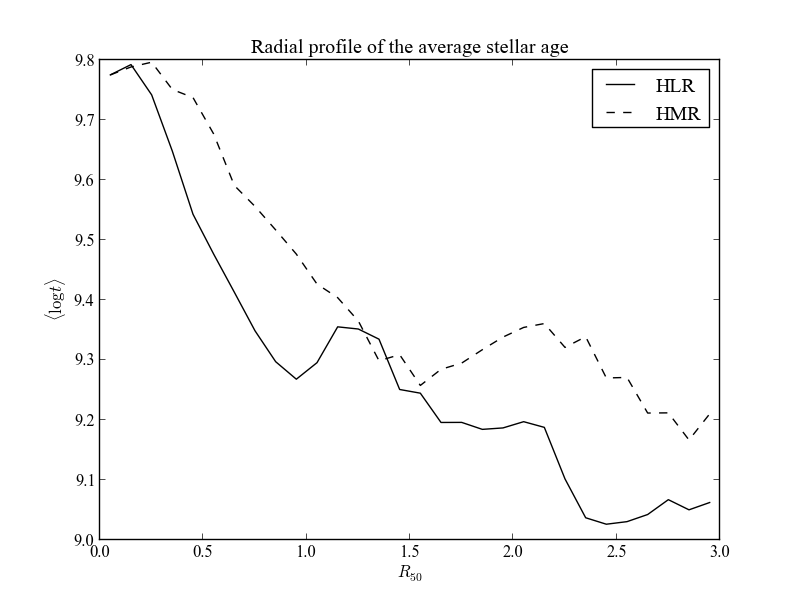
Now let’s explain the procedure. bin_r represent the bin boundaries in which we want to calculate the mean value of the property. It is not suitable for plotting, as it contains one extra value (len(bin_r) == len(at_flux__HLR) + 1). So, we calculate the central points of the bins, bin_center. Then, we proceed to calculate the radial profile of at_flux__yx, which is the average log. of the age, weighted by flux. We do so using HLR and HMR as a distance scale. The mass is usually more concentrated in the center of the galaxy, so that in general HMR < K.HLR_pix and therefore the plots look similar, but stretched.
Calculating the radial profile of a N-D image¶
In the example above we compute the radial profile of a 2-D image. Now, the process is the same for higher-dimensional images. The presentation can be tricky, though. Let’s see an example.
We have the surface distribution of mass in ages, McorSD__tyx, which is a 3-D array (age, y, x). One may be tempted to do a for loop for each age, but the method radialProfile() takes care of this, as it accepts properties with more than 2 dimensions, as long as the spatial dimensions are the rightmost ([..., y, x] in numpy slice notation). In this example, we want to plot a 2-D map of the mass as a function of radius and age. We will use the Half Light Radius as a radial scale, so we don’t have to set the argument rad_scale as we did previously. We also don’t need the bin centers, as the plot method used is fit for dealing with histogram-like data.
>>> bin_r = np.arange(0, 2.5+0.1, 0.1)
>>> McorSD__tyx = K.McorSD__tZyx.sum(axis=1)
>>> logMcorSD__tr = np.log10(K.radialProfile(McorSD__tyx, bin_r, mode='mean'))
>>> vmin = -2
>>> vmax = 4
>>> plt.pcolormesh(bin_r, K.logAgeBaseBins, logMcorSD__tr, vmin=-2, vmax=4)
>>> plt.colorbar()
>>> plt.ylim(K.logAgeBaseBins.min(), K.logAgeBaseBins.max())
>>> plt.ylabel(r'$\log t$')
>>> plt.xlabel(r'$R_{50}$')
>>> plt.title(r'$\log M_{cor} [M_\odot / pc^2]$')
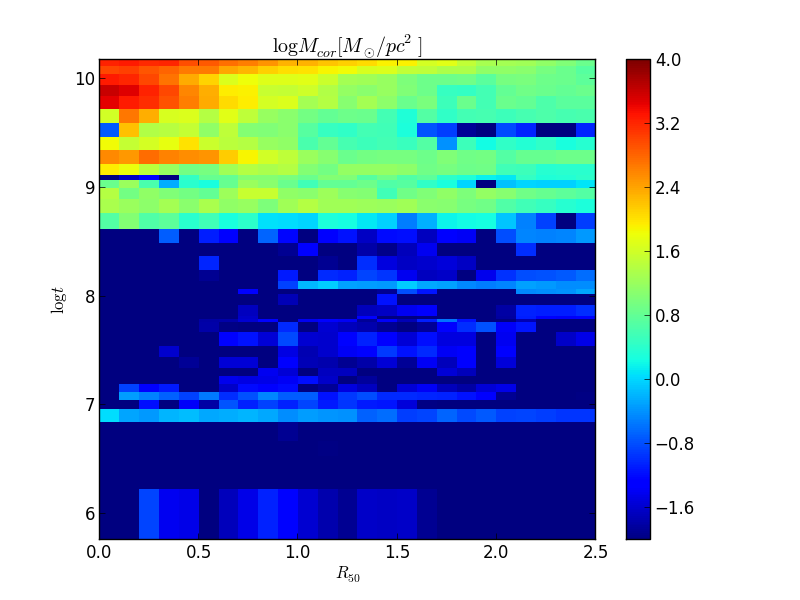
As we said, the :meth:pseudocolor method needs the bin edges, so we have to use the radial bin edges (provided by bin_r), and the age bin edges. The property called logAgeBaseBins returns the age bin edges in log space, see it’s documentation for more details.
One can also compute the sum of the values (or the mean or median) inside a ring, using a pair of values as bins:
>>> Mcor_tot_ring = K.radialProfile(K.McorSD__yx, \
(0.5, 1.0), mode='sum') * K.parsecPerPixel**2
The rightmost term is the pixel area, to convert from surface density to absolute mass. The mode keyword indicates what to do inside the bins. By default, the mean is computed. The valid values for mode are:
- 'mean'
- 'mean_exact' (see below)
- 'sum'
- 'median'
If the number of pixels inside each radial bin is needed, the keyword argument return_npts may be set. In this case, the return value changes to a tuple containing the radial binnned property and the number of points in each bin.
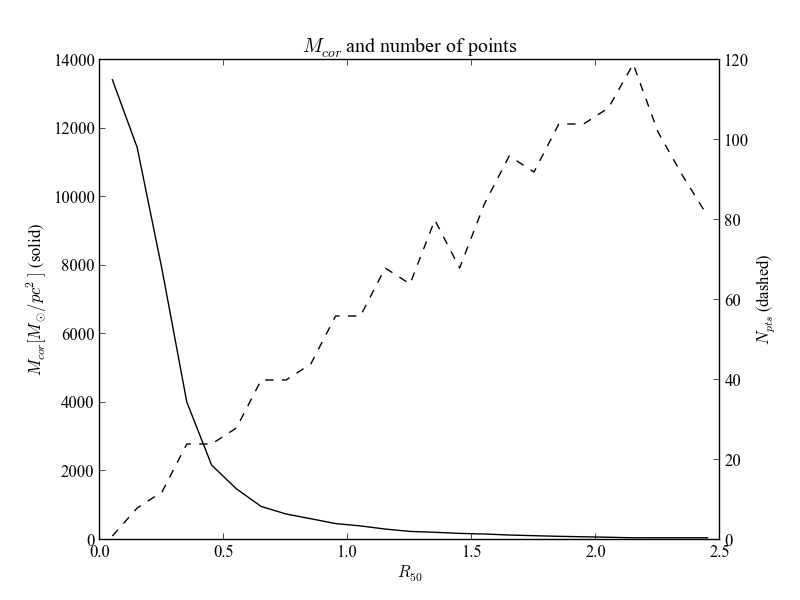
>>> bin_r = np.arange(0, 2.5+0.1, 0.1)
>>> bin_center = (bin_r[1:] + bin_r[:-1]) / 2.0
>>> McorSD__r, npts = K.radialProfile(K.McorSD__yx, bin_r, return_npts=True)
>>> fig = plt.figure()
>>> plt.title('$M_{cor}$ and number of points')
>>> ax1 = fig.add_subplot(111)
>>> ax1.plot(bin_center, McorSD__r, '-k')
>>> ax1.set_xlabel(r'$R_{50}$')
>>> ax1.set_ylabel(r'$M_{cor} [M_\odot / pc^2]$ (solid)')
>>> ax2 = ax1.twinx()
>>> ax2.plot(bin_center, npts, '--k')
>>> ax2.set_ylabel(r'$N_{pts}$ (dashed)')
Radial profiles using exact apertures¶
All the radial profiles calculated above suffer from a “jagginess” caused by the discrete method of assigning pixels to the radial bins (see the dashed line from the image above). When pixels fall in the boundaries of the bins, the whole pixel gets assigned to one or the other bin, based onthe pixel center. Often this is harmless, but for small radii (or conversely, large pixels) this effect can be a problem. The solution in this case is to “split” the pixel between the bins, calculating the intersection of the bin boundaries and each pixel. Needless to say, this can be very slow. To use the exact apertures algorithm (shamelessly “stolen” from photutils), change the mode parameter to 'mean_exact'.
Here we can see a comparison between the exact and the discrete versions of the radial profile of the luminosity weighted mean stellar age.
>>> bin_r = np.arange(0, 2.5+0.1, 0.1)
>>> bin_center = (bin_r[1:] + bin_r[:-1]) / 2.0
>>> atflux, npts = K.radialProfile(K.at_flux__yx, bin_r, \
mode='mean', return_npts=True)
>>> atflux_ex, npts_ex = K.radialProfile(K.at_flux__yx, bin_r, \
mode='mean_exact', return_npts=True)
>>> fig = plt.figure()
>>> plt.title(r'$\langle \log t \rangle_L$ and number of points: discrete vs. exact')
>>> ax1 = fig.add_subplot(111)
>>> ax1.plot(bin_center, atflux, '-k', label='discrete')
>>> ax1.plot(bin_center, atflux_ex, '-r', label='exact')
>>> ax1.set_xlabel(r'$R_{50}$')
>>> ax1.set_ylabel(r'$\langle \log t \rangle_L [yr]$ (solid)')
>>> plt.legend(loc='lower right')
>>> ax2.plot(bin_center, npts_ex, '--r')
>>> ax2 = ax1.twinx()
>>> ax2.plot(bin_center, npts, '--k')
>>> ax2.set_ylabel(r'$N_{pts}$ (dashed)')
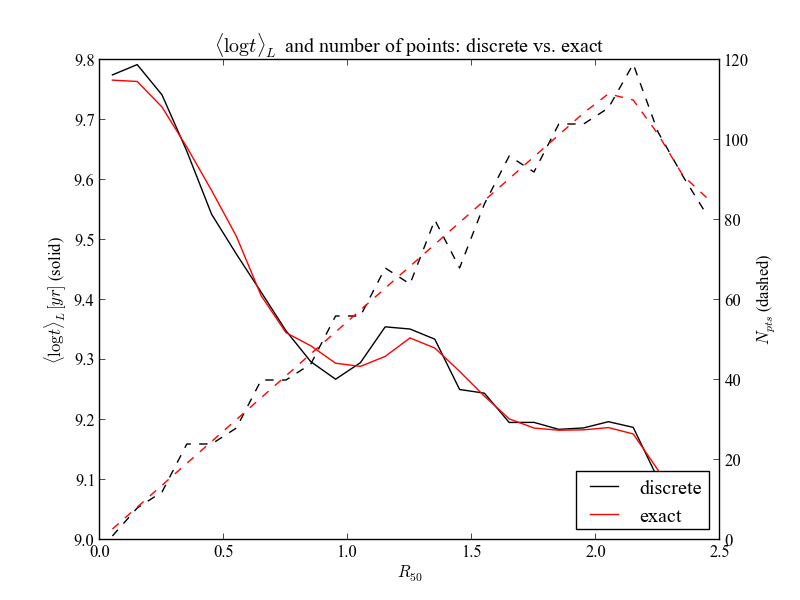
The bin area (dashed lines, right vertical axis) is much smoother when using the 'mean_exact' algorithm (in red), compared to the discrete 'mean' version (in black). As you can see, the age radial profile (solid lines, left vertical axis) becomes less noisy.
Azimuthal and radial profile of a N-D image¶
Still more generic than radialProfile() is azimuthalProfileNd(). It adds the capability of azimuthal profiles, based on the angles associated with each pixel. This angle is accessible using pixelAngle__yx, in radians. The method getPixelAngle() allows one to get the angle in degrees, or to get an arbitraty ellipse geometry, much like getPixelDistance().
In PyCASSO the pixel angle is defined as the counter-clockwise angle between the pixel and the semimajor axis, taking the ellipse distortion into account. Please look at getPixelAngle() for more details.
In the example below, we calculate the azimuthal profile of the log. age, averaged in flux, inside three rings between 0.5, 1.0, 1.5 and 2.0 HLR.
>>> bin_a = np.linspace(-np.pi, np.pi, 21)
>>> bin_a_center_deg = (bin_a[1:] + bin_a[:-1]) / 2.0 * 180 / np.pi
>>> bin_r = np.array((0.5, 1.0, 1.5, 2.0))
>>> at_flux__ar = K.azimuthalProfileNd(K.at_flux__yx, bin_a, bin_r)
>>> plt.plot(bin_a_center_deg, at_flux__ar[:,0], '-r', label='0.5 > r(HLR) > 1.0')
>>> plt.plot(bin_a_center_deg, at_flux__ar[:,1], '-g', label='1.0 > r(HLR) > 1.5')
>>> plt.plot(bin_a_center_deg, at_flux__ar[:,2], '-b', label='1.5 > r(HLR) > 2.0')
>>> plt.title('Azimuthal profile of mean stellar age')
>>> plt.ylabel(r'$\langle \log t \rangle_L$')
>>> plt.xlabel(r'$\theta\ [degrees]$')
>>> plt.legend()
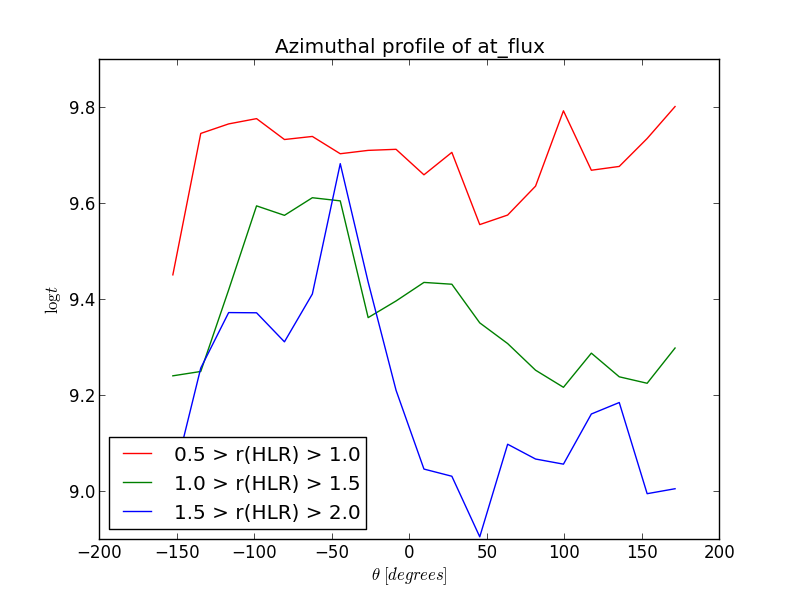
Filling missing data¶
The example galaxy used above does not have any masked foreground or background objects. This is not always the case. For example, galaxy K0277 (NGC2916) has a foreground star near it’s center, which was masked in the analysis pipeline.
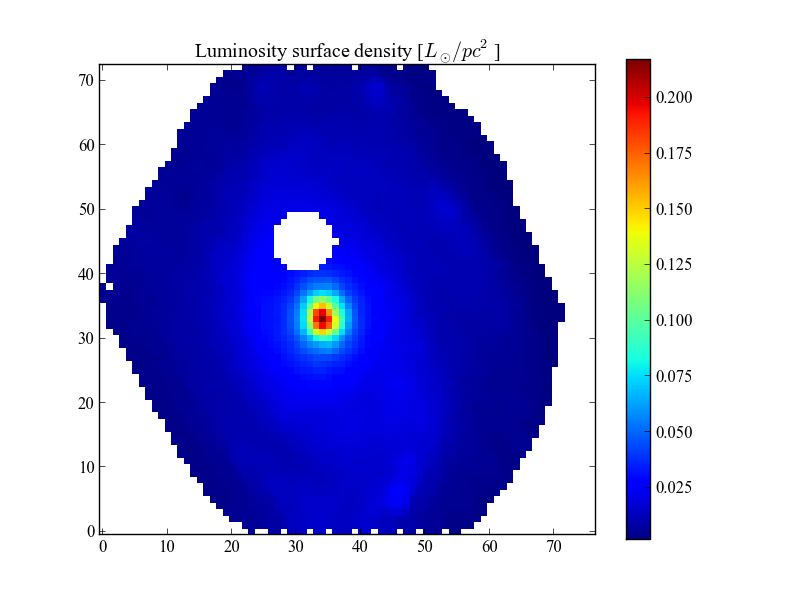
This impacts some measurements like the total mass of the galaxy or the cumulative radial curves. The latter can have a big effect in properties like the half light radius. To take the hollow areas into account, we can use the method fillImage(). By default, it takes a property as input, calculates its radial profile and interpolates the missing data from the radial profile. This assumes the user already called setGeometry() with proper values. Alternatively, one can calculate a radial profile and use it as parameter when filling, see the documentation. Also, there’s two modes of filling: 'hollow' and 'convex'. The first one only fills the hollow pixels, while the second fills the complete convex hull of the image (that is, fills the edges making the image “roundy”). Here’s the same image as above, filling the convex hull.
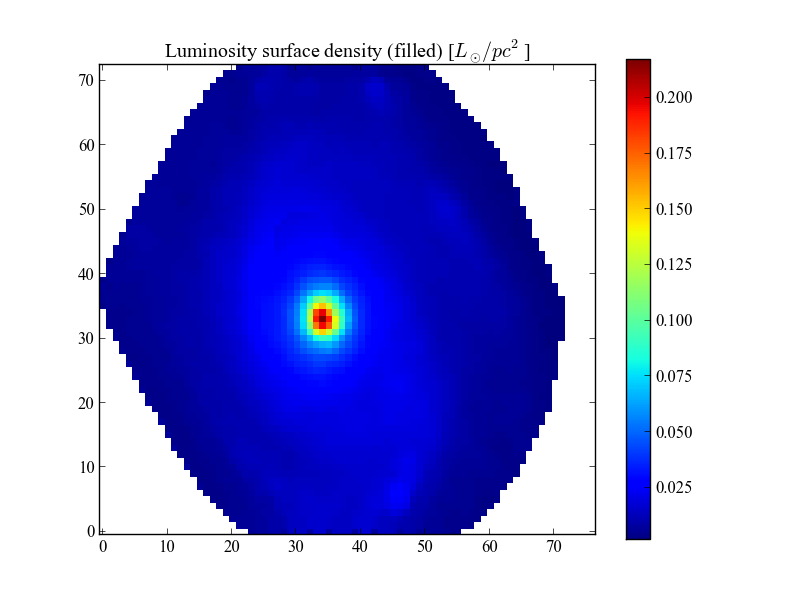
Note the barely visible artifact in the filled areas. As an example, let’s compare the values of the half light radius with and without filling. We will calculate the filling by hand to illustrate the usage. The methods getHalfRadius() and getHLR_pix() have a fill parameter, which when set to True, will perform the filling automatically.
>>> pa, ba = K.getEllipseParams()
>>> K.setGeometry(pa, ba)
>>> LobnSD_fill, mask = K.fillImage(K.LobnSD__yx, mode='hollow')
>>> K.getHalfRadius(LobnSD_fill, mask=mask)
19.43191121094409
>>> K.getHalfRadius(K.LobnSD__yx)
19.991108029801655
If one does not fill the hollow areas, the computed half light radius will be overestimated (in this case, by about 0.5 pixel, but it can be worse). The same applies to the total mass or luminosity of the galaxy.
Working with spectra¶
PyCASSO handles the stellar synthesis results from IFS data. One of the products of the stellar synthesis is a synthetic spetrum of each pixel (f_syn__lyx), containing only the stellar contribution to the light. The observed spectra (f_obs__lyx), errors (f_err__lyx) and flags (f_flag__lyx) are also available. Using these, one can easily, for example, obtain the residual spectra and measure emission lines.
>>> f_syn_nuc = K.f_syn__lyx[:, K.y0, K.x0]
>>> f_obs_nuc = K.f_obs__lyx[:, K.y0, K.x0]
>>> f_flag_nuc = K.f_flag__lyx[:, K.y0, K.x0]
>>> mask = f_flag_nuc < 1.0
>>> ax1 = plt.subplot(211)
>>> ax1.plot(K.l_obs[mask], f_obs_nuc[mask], '-k', label='Obs.')
>>> ax1.plot(K.l_obs[mask], f_syn_nuc[mask], '-r', label='Syn.')
>>> ax1.set_xlabel(r'wavelength $[\AA]$')
>>> ax1.set_ylabel(r'Flux $[erg / s / cm^2 / \AA]$')
>>> ax1.set_title('Spectra')
>>> ax1.legend()
>>> ax2 = plt.subplot(212)
>>> ax2.plot(K.l_obs[mask], f_obs_nuc[mask] - f_syn_nuc[mask], '-k')
>>> ax2.set_xlabel(r'wavelength $[\AA]$')
>>> ax2.set_ylabel(r'Flux $[erg / s / cm^2 / \AA]$')
>>> ax2.set_title('Residual')
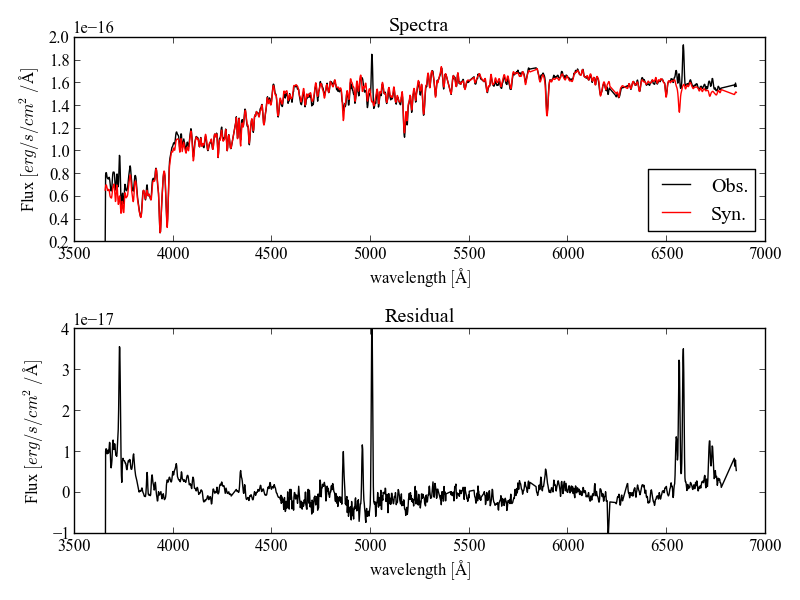
Notice the emission lines are more evident in the residual. Thus using PyCASSO it is possible to analyze the spatially resolved spectral features like the \(D_n(4000)\) and Lick indices.
Integrated properties¶
In addition to the spatially stellar synthesis, we performed the stellar synthesis in the integrated spectra of the galaxies. This was one can check if the sum of the parts is equal to the whole. In general the properties in integrated form contain the prefix integrated_. Please take a look at the section Galaxy property list. Let’s take a look in the mass of the galaxy.
>>> K.integrated_Mcor / 1e10
6.4588941491889695
>>> (K.McorSD__yx * K.parsecPerPixel**2).sum() / 1e10
6.7011924815290183
>>> K.integrated_Mcor / (K.McorSD__yx * K.parsecPerPixel**2).sum()
0.9638425051947227
That is, the total mass of the galaxy, calculated using the stellar synthesis of the integrated spectra (integrated_Mcor) is 4% smaller than the sum of the masses of the pixels, calculated in the same way.