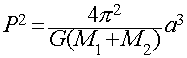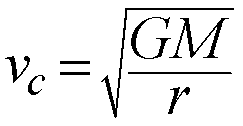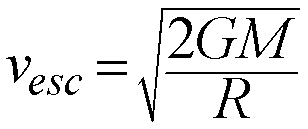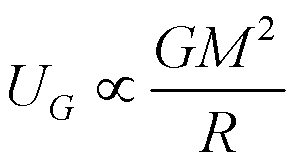Astronomy 162:
Introduction to Stars, Galaxies, & the Universe
Prof. Richard Pogge, MTWThF 9:30

Matter & Gravity

Readings: Ch 5, section 5-7, Ch 4, sections 4-7 & 4-8

Key Ideas

Structure of Atoms: Nuclei of protons & neutrons orbited by electrons; Elements, Isotopes, & Radioactivity
Four Fundamental Forces: Strong & Weak Nuclear Forces; Electromagnetic & Gravitational Forces
Nature of Gravity: Inverse Square Law; Orbits & Circular Speed; Escape Speed & Gravitational Binding Energy

Matter

Ordinary matter encompasses a wide range of phenomena:

Fundamental particles (quarks & leptons)
Subatomic particles (protons & neutrons) composed of fundamental particles
Single atoms composed of protons, neutrons, & electrons (Hydrogen, Helium, Gold, etc.)
Simple molecules composed of 2 or more atoms bound together
Macromolecules (DNA, complex polymers)
Macroscopic objects (rocks, people, planets ...)

Most ordinary matter in the universe is in the form of atoms.

Atoms

Atoms consist of two basic parts:

Nucleus of heavy subatomic particles:

proton: positively charged
neutron: uncharged (neutral)

Cloud of Electrons orbiting the Nucleus:

negatively charged particles (leptons)
masses are 1/1836^th the mass of a proton

Atoms are mostly empty space:

Only 1 part in 10¹⁵ of the volume is occupied.
Volume is threaded by electromagnetic fields.

A simple, yet familiar cartoon:
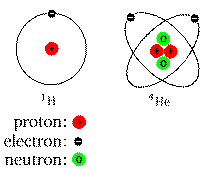
Simple Atoms (Schematic)

Real atoms don't look like this, but it can help you visualize the locations and numbers of the different components (nucleus and electrons).

Chemical Elements

We distinguish atoms into Elements by the total number of protons in their nucleus.

Atomic Number:

1 proton = Hydrogen
2 protons = Helium
3 protons = Lithium ... and so on

Number of electrons = Number of protons

All elements are Chemically Distinct

Top Ten Most Abundant Elements

10) Sulfur

9) Magnesium

8) Iron

7) Silicon

6) Nitrogen

5) Neon

4) Carbon

3) Oxygen

2) Helium

1) Hydrogen

In general, the ordinary matter in the Universe is mostly Hydrogen and Helium (roughly 75% and 24%, respectively), and 1% every other element.

Known Elements

There are 117 elements currently known from laboratory studies:

87 are metals
11 are gasses
2 occur as liquids (Bromine & Mercury)
26 are radioactive
24 are made only in the lab

In addition, each element can have a number of isotopes.

The two newest members of the table of the elements, with atomic numbers of 113 and 115, were recently made in accelerators in Russia.

Isotopes

A given element can have many different Isotopes

Same number of protons.
Different number of neutrons.

Example: Carbon Isotopes:

¹²C has 6 protons and 6 neutrons

¹³C has 6 protons and 7 neutrons

¹⁴C has 6 protons and 8 neutrons

All isotopes of a given element are chemically identical, but they have different masses.

Radioactivity

If a nucleus has too many or too few neutrons, it becomes unstable to radioactive decay

Examples:

    ³H (1p+2n) -> ³He (2p+1n) + e^- + neutrino

    ¹⁴C (6p+8n) -> ¹⁴N (7p+7n) + e^- + neutrino 
                      (basis of radioactive carbon dating)

Free neutrons are also unstable:

    n -> p + e^- + neutrino

All of the above are examples of "beta decay", in which one of the neutrons turns into a proton, shedding its excess mass by spitting out an electron and a neutrino.

The Fundamental Forces

All interactions among matter are governed by four fundamental forces:

Strong & Weak Nuclear Forces: Bind protons to neutrons inside nuclei; Mediate nuclear reactions and radioactivity
Electromagnetic Force: Binds electrons to nuclei inside atoms, and atoms to atoms inside molecules; Mediates chemical reactions
Gravitational Force: Binds massive objects together on large scales; Mediates orbital motions

Gravitation

Gravitation binds matter to matter over long distances:

Long-range attractive force
Weakest force of nature.
Obeys the Inverse Square Law of distance:

Gravitational Force

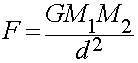
The Force of Gravity between any two objects depends only upon:

The masses of the two objects:

More massive objects exert a stronger the gravitational force.

The distance between them:

The force gets stronger as the two objects move closer together.
The force gets weaker as the two objects move farther apart.

It does not depend on the shapes, colors, or compositions of the objects.

Kepler's Third Law

Kepler's 3^rd (or "Harmonic") Law of orbital motions

P² = a³

only applies to planets orbiting our Sun.

Newton, however, derived a more general version

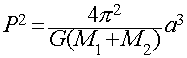
This is a universal form of Kepler's 3rd law applicable to any two massive objects orbiting each other anywhere in the Universe.

The important quantities in this form are:: P = period of the orbit; a = semi-major axis of the orbit; M₁+M₂ = combined masses of the two bodies

This gives us a way of measuring the masses of objects from observation of their orbital period and semi-major axis.

Circular Speed

In the simple case of a tiny mass in a circular orbit around a more massive body we can simplify the formula above to define the smaller object's Circular Speed:

Circular Speed: Speed needed to sustain a circular orbit at a given distance from a massive object:

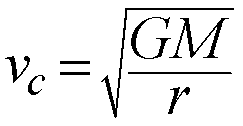
The circular speed depends on two things:

The mass of the larger parent body (M)
The radius of the orbit (r)

This gives us another way to measure masses for objects in circular orbits around larger bodies, now measuring orbital speeds (Doppler Effect) and orbital radii.

In general, orbital motions are the most important way we have to estimate the masses of astronomical objects.

Escape Speed

Another consequence of gravitating bodies is that there is a minimum speed an object must be given in order for it to escape from the gravity of its parent body.

This is called the Escape Speed:

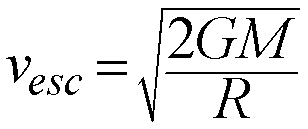
The escape speed depends on the Mass of the body (M) and its radius (R). Basically, the stronger the gravity at the surface of a body, the faster you have to be going to escape from its gravitational clutches.

Examples:

Earth's Surface: V_esc = 11.2 km/sec (40,320 km/hr)
Sun's Surface: V_esc = 615 km/sec (~2.2 Million km/hr)

Gravitational Binding Energy

Imagine you wanted to take apart a gravitating body. You might do it piece-by-piece, taking a rock and throwing it with the escape speed. As the body got steadily smaller, the escape speed would be less.

If you added up all the energy you would need for each piece, you would derive the Gravitational Binding Energy for the body:

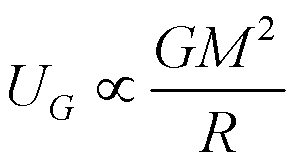
This depends on two quantities: the Mass (M) and the Radius (R) of the body.

The formula above is a "proportionality", it tells us how the binding energy scales with the mass and radius of the object. The constant out front we need depends on details of how matter is distributed in the object. For example, a sphere of uniform density would have a constant of 3/5.

For the Earth, the Gravitational Binding Energy is about 2x10³² Joules, or about 12 days of the Sun's total energy output!

Implications

For objects of the same Radius but with different masses, the more massive object will have

Faster orbital and escape speeds
Greater gravitational binding energy ("more tightly bound")

For objects of the same Mass but different Radii, the larger object (bigger radius) will have:

Slower circular and escape speeds
Less gravitational binding energy ("less tightly bound")

Gravity: The Universal Glue

Gravity is the force that rules in the domain of astrophysics:

Holds planets and stars together
Controls the orbits of moons around planets
Controls the orbits of planets around stars
Binds stars into galaxies
Binds galaxies into groups and clusters
Binds galaxy clusters into superclusters
Binds the Universe together...

Throughout this course we will be exploring the consequences of gravitation.

Return to [ Introduction Index | Astronomy 162 Main Page ]