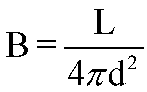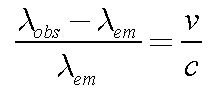|
Astronomy 162:
Introduction to Stars, Galaxies, & the Universe
Prof. Richard Pogge, MTWThF 9:30
|
Lecture 2: Light the Messenger
Readings: Chapter 5, sections 5-1, 5-2, & 5-9
- Light is Electromagnetic Radiation
- Light as Waves and Photons
- Electromagnetic Spectrum
- Sequence of photon energies
- Luminosity vs. Apparent Brightness
- Inverse Square Law of Brightness
- Doppler Effect
- Due to relative motion between source & observer
- Way to measure speeds at a distance
Electromagnetic Radiation
Light is Electromagnetic Radiation, a self-propagating
Electromagnetic disturbance that moves at the speed of light
Can treat light as either:
- Electromagnetic Waves
- Photons (particles of light)
Wave Nature of Light
Can treat light as an Electromagnetic Wave
- Regular fluctuation in the intensity of coupled electric and
magnetic fields.
- Wave travels through a vacuum at the speed of light.
- Doesn't need a medium to "wave" in.
The speed of light (c) is the same for all light waves:
c = 299,792.458 km/sec
This speed is independent of the wavelength or frequency of the
light!
Particle Nature of Light
We can also treat light as particles or Photons.
Photon:
- Massless particles that carry energy at the speed of light.
Photons are characterized by their Energy, which is
proportional to their Frequency, f.
Photon Energy:
E = hf
where: f = frequency of the light, and h = Planck's
Constant
In words:
Higher Frequencies mean Higher Energies
Note: Energy, E, is a "particle property", whereas frequency, f,
is a "wave property". They are related through Planck's Constant, h.
Planck's constant is one of the "Fundamental Constants" of Nature
(another one we've met in this lecture is the speed of light, c). One
can think of Planck's constant as serving as the "link" between the wave
and particle natures of light, and indeed h is the fundamental constant
in "quantum mechanics", the modern view of matter and radiation as
entities ("quanta") that have the properties of both waves and
particles.
The Electromagnetic Spectrum
The sequence of photon energies running from low energy to high
energy is called the Electromagnetic Spectrum
low energy = low frequency = long wavelength
- Examples:
- Radio Waves, Infrared
high energy = high frequency = short wavelength
- Examples:
- Ultraviolet, X-rays, Gamma Rays
Major Divisions of the Electromagnetic Spectrum
| Type of Radiation | Wavelength Range |
| Gamma Rays | <0.01 nm |
| X-Rays | 0.01-10 nm |
| Ultraviolet | 10-400 nm |
| Visible Light | 400-700 nm |
| Infrared | 700-105 nm (0.1 mm) |
| Microwaves | 0.1-10mm |
| Radio | >1 cm |
The Visible Spectrum
This is all forms of light we can see with our eyes.
- Wavelengths: 400 - 700 nanometers (nm)
- Frequencies: 7.5x1014 - 4.3x1014 waves/second
We sense visible light of different energies as different colors.
The basic colors of the visible spectrum are defined roughly as follows,
in order of increasing photon energy:
| |
|
|
|
|
|
|
|
| Color Name |
Red |
Orange |
Yellow |
Green |
Blue |
Indigo |
Violet |
Approximate
Wavelength |
700nm |
650nm |
600nm |
550nm |
500nm |
450nm |
400nm |
You can remember the order of these colors from lowest to highest
energy using the famous mnemonic: ROY G. BIV
Important Note:
The wavelengths given in the table above are only approximate. Color
is a physiological response of our brains to visible light of different
energies. Our division of the visible spectrum into named colors is very
subjective, and certainly not a matter of even divisions every 50 nm of
wavelength! I include approximate wavelengths primarily for purposes of
illustration. An oft-cited example of the subjectivity of color names is
the color "orange". It did not enter the language until the
Middle Ages, when the fruit of the same name reached Europe from the
Middle East. Before that, the color would have been called a reddish
shade of yellow.
How "Bright" is a Light Source?
We need to quantify how bright a light source is. The most convenient
way is using the photon picture for light:
- "Brightness" measures the number of photons per second emitted by the
light source
There are two ways to quantify this:
- Luminosity (L):
- Measure of the total energy output:
- L is measured in Power Units (energy/sec) like Watts
- L is independent of distance
- Luminosity is an intrinsic property of the light source.
- Apparent Brightness (B):
- Measures how bright an object appears to be as seen from
a distance
- B is measured in Flux Units (energy/sec/area)
- B depends on the distance to the source
- Brightness is what we actually measure (an observable property).
Luminosity and Brightness are related through the Inverse Square Law
of Brightness:
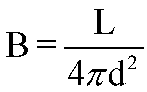
In words:
- Apparent Brightness is inversely proportional to the
square of the distance to the source
Implications:
- If the source is 2x closer, it appears 4x brighter.
- If the source is 2x farther away, it appears 4x fainter.
This law is extremely important to us in astronomy.
The Doppler Effect
Change in observed wavelength of a wave when the source of the
waves and observer are moving relative to each other.
Examples:
- Sound Waves (Siren or Train Horn)
- Light Waves
The amount of the shift and its sign depends on
- relative speed of the source & observer
- direction of motion (together or apart)
Doppler Effect in Sound
Two cats are sitting between a windup mouse toy that emits an electronic
squeak. The mouse is moving towards the left towards the first cat and
away from the second:
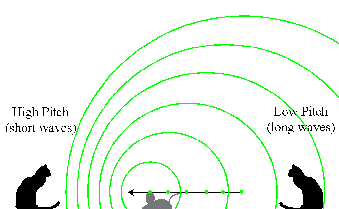
The mouse emitted a squeak when it was at the location of each of the
green dots. The sound wave ("squeak!") moves outward spherically from
each point of emission. Because the mouse is moving, the sound waves
have different emission centers. Those waves ahead of its motion
(towards the left) are are scrunched together, while those behind are
spread out.
Results:
- The cat on the left hears a higher-pitched squeak because the waves
have a shorter wavelength (scrunched together by the mouse's motion).
- The cat on the right hears a lower-pitched squeak because the waves
have a longer wavelength (spread out by the mouse's motion).
Doppler Effect in Light
The Doppler Effect in light works the same way as it does for sound:
- Moving away from the observer, wavelength gets longer:
REDSHIFT
- Moving towards the observer, wavelength gets shorter:
BLUESHIFT
A Way to Measure Speeds
Observe the wavelength
lobs of a
light source with a known emitted wavelength
lem.
The difference between the observed and emitted wavelengths is
directly proportional to the speed of the source towards or away from
you (v), given by the Doppler Formula:
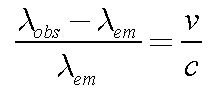
Here c is the speed of light.
- The size of the shift gives the speed of the source
- The color of the shift (Red or Blue) gives the direction of motion
(away or towards you).
The Doppler Effect in Practice
The Doppler Effect in light is used by astronomers to measure the speeds
of objects moving towards or away from the Earth.
But, we also use the Doppler Effect in light in everyday settings. Some
examples:
- Traffic Radar Guns:
- Radar gun bounces a pulse of microwaves (or infrared laser light)
of a known wavelength off a car or truck, measure the wavelength
reflected back. The Doppler shift gives the vehicle's speed.
- Doppler Weather Radar:
- Similar principle, bounce microwave radar signals of known
wavelength off of clouds, measure the wavelength reflected back. The
Doppler shift and its sign (blue or red) gives the speed and direction
of the clouds. The strength of the returned signal also gives the
amount of rain or snow falling.
Light the Messenger
The properties of light give us a way to bridge the vast distances
between us and astronomical objects.
The light "encodes" important information about the source of the light
- Luminosity measures how much energy the object emits in the
form of light.
- Doppler Shift tells us how fast it is moving towards or away from us
To learn more from light, however, we need to understand how light and
matter interact, which is the subject of the next
lecture.
Return to [
Introduction Index
|
Astronomy 162 Main Page
]
Updated: 2006 January 2
Copyright © Richard W. Pogge,
All Rights Reserved.