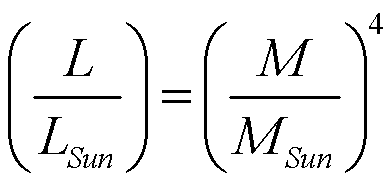|
Astronomy 162:
Introduction to Stars, Galaxies, & the Universe
Prof. Richard Pogge, MTWThF 9:30
|
Lecture 11: The Internal Structure of Stars
Readings: none(!)
- Observational Clues to Stellar Structure:
- H-R Diagram
- Mass-Luminosity Relationship
- Hydrostatic Equilibrium
- Balance between Gravity & Pressure
- Core-Envelope Structure of Stars
- Hot, dense, compact core
- cooler, low-density, extended envelope
From Stellar Properties to Stellar Structure
Any successful theory of stellar structure must explain the observed
properties of stars.
Seek clues in correlations among the observed properties,
in particular:
- Mass
- Luminosity
- Radius
- Temperature
The Hertzsprung-Russell Diagram
Recall the Hertzsprung-Russell (H-R)
Diagram introduced back in Unit 1. This is a
plot of Luminosity vs. Temperature for stars:
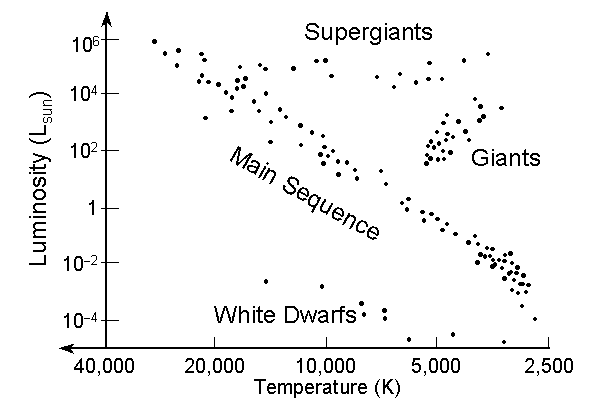
The most prominent feature of the H-R diagram is the Main Sequence (M-S):
- Strong correlation between Luminosity and Temperature.
- Hotter stars are Brighter than cooler stars along the M-S.
- About 85% of nearby stars, including the Sun, are on the M-S.
All other stars differ in size:
Giants & Supergiants:
- Very large radius, but same masses as M-S stars
White Dwarfs:
- Very compact stars: ~Rearth but with ~0.6 Msun!
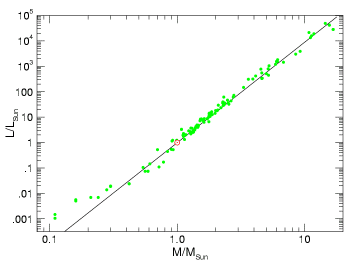
If we make a plot of Luminosity vs. Mass for the Sun and all Main
Sequence stars in binary systems that have good mass measurements, we
that a Main Sequence star's Luminosity is very strongly correlated with
its Mass:
This strong correlation is called the Mass-Luminosity
Relationship. It is expressed mathematically as:
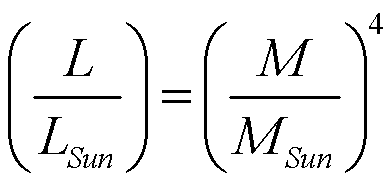
In words:
- "More massive M-S stars are more luminous."
This relation is only true for Main Sequence stars: Giants,
Supergiants, and White Dwarfs do not follow the Mass-Luminosity
relation.
The graph above shows data for the Sun and 121 binary stars for which
there are reliable mass estimates (mostly eclipsing binaries with some
nearby visual binaries, particularly at the low-mass end). Clicking on
the plot will show a full-size version. The line drawn is the best-fit
M-L relation.[11.1]
Mean Stellar Density
The mean density[11.2] of a star is:
- Mean Density = Mass / Volume
Main Sequence: small range of mean densities
- Sun (G2v): ~1.6 g/cc
- O5v Star: ~0.005 g/cc
- M0v Star: ~5 g/cc
Giants: Low-density stars: ~10-7 g/cc (e.g., K5III)
Supergiants: Very low-density: ~10-9 g/cc (e.g., M2I)
White Dwarfs: High-density stars: ~105 g/cc
For reference, at sea level on Earth, water has a density of 1 g/cc,
and air has a density of ~0.001 g/cc.
Interpreting the Observations:
For Main-Sequence Stars:
- Strong L-T Relationship on H-R Diagram
- Strong M-L Relationship
Implies that they have similar structures & governing laws.
Giants, Supergiants, and White Dwarfs must have very different internal
structures from M-S stars of similar mass.
Laws of Stellar Structure I: The Ideal Gas Law
Most stars obey the Ideal Gas Law:[11.3]
- Pressure = Density x Temperature
In words:
- Compressing a gas results in higher P & T
- Expanding a gas results in lower P & T
Tells us how changes in the internal Temperature of a star
affects its internal Pressure.
Laws of Stellar Structure II: The Law of Gravity
Stars are very massive & bound together by their Self-Gravity
- Gravitational Binding Energy increases as 1/R
In words:
- As a star contracts, it becomes more gravitationally bound.
- As a star expands, it becomes less gravitationally bound.
Two opposing forces are at work within a star:
- Gravity pulling inward wants to make the star contract.
- Pressure pushing outwards wants to make star star expand.
Pressure & Gravity work on each other:
- Gravity confines the gas in the star against Pressure expansion.
- Pressure supports the star against Gravitational collapse.
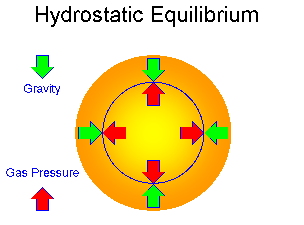
When there is exact balance between the two, we have a condition of
Hydrostatic Equilibrium.
In this condition, the star neither expands nor contracts.
Core-Envelope Structure
Outer layers press down on the inner layers.
- The deeper you go into a star, the greater
the pressure.
The Gas Law says:
- Great pressure = hotter, denser gas
The consequence is that the star develops a Core-Envelope structure:
- A hot, dense, compact central CORE surrounded by
- A cooler, lower density, extended ENVELOPE

Example: The Sun
Core:
- Radius = 0.25 Rsun
- T = 15 Million K
- Density = 150 g/cc
Envelope:
- Radius = Rsun = 700,000 km
- T = 5800 K
- Density = 10-7 g/cc
The Essential Tension
The life of a star is a constant tug-of-war between Gravity &
Pressure.
Tip the internal balance either way, and it will change the star's
outward appearance. This establishes an important principle for
how stars work:
- Internal Changes have External Consequences
Thus, changes in the interior conditions of stars will be reflected in
their outward appearances, and hence affect where they will be located
in the H-R Diagram.
Return to [
Unit 2 Index
|
Astronomy 162 Main Page
]
Updated: 2006 January 15
Copyright © Richard W. Pogge,
All Rights Reserved.